The May-Leonard Systems¶
The May-Leonard systems are a rich set of models for stochastic spatial models based on non-transitive competition among species. The original May-Leonard system was a set of ordinary differential equations simulating a fully-connected system of three species in a rock-paper-scissors relationship, where species 1 defeated species 2 defeated species 3 defeated species 1. The original equations lead to unstable oscillations, which lead to two species going extinct in a system of finite size - but in a spatially-explicit system, provided the diffusion mobility is low enough, all three species can coexist and form fascinating spiral shapes.
The generalized \((N, r)\) May-Leonard system was defined in Roman, Dasgupta, and Pleimling 2013 to be a system with \(N + 1\) states: 0 denoting an empty sites and \(1, 2, ..., N\) states denoting different species. Species \(k\) predates on species \(k + 1, k + 2, ..., k + r\), where addition is performed modulo - so, in a \((6, 2)\) May-Leonard system, species 5 predates on species 6 and species 1. The system then has the following transitions:
Reproduction: \((i,0)\to(i,i)\) and \((0,i)\to(i,i)\) at rate 0.1.
Diffusion: \((i,j)\to(j,i)\) at rate \(\mu\), where \(\mu\) is a hyperparameter.
Predation: \((i,j)\to(i,0)\) and \((j,i)\to(0,i)\) at rate 0.1 if \(i\) predates on \(j\).
(Note that our rates are different from the rates in the original paper because of how we define the transitions as ordered pairs and then make them symmetric.)
The May-Leonard systems show quick coarsening into domains consisting of fewer species. For example, the \((3, 1)\) May-Leonard system forms:

In some cases, the domains may consist of alliances of multiple species. For example, in the \((4, 1)\) May-Leonard system, species 1 and 3 do not predate on each other, nor do species 2 and 4, so they form a pair of mixed domains:
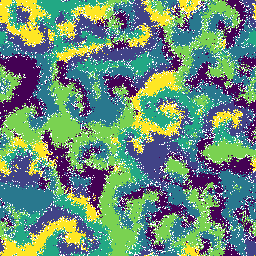
Another interesting system is \((6, 3)\), where we see the formation of two domains, and then the formation of subdomains with spiral patterns inside the larger domains: